À quoi ça sert le second degré ? C’est vrai ça ! Après tout, pourquoi nous enseigner cette notion en cours de maths en première spécialité ?
Je vais vous présenter dans cet article plusieurs cas où le second degré est nécessaire.
À quoi sert le second degré: d’abord, quelques rappels…
Je rappelle que le second degré est une notion concernant les polynômes de la forme \(P(x)=ax^2+bx+c\).
Cette théorie nous dit que les racines du polynômes sont égales à :$$x_1=\frac{-b-\sqrt{\Delta}}{2a}\quad;\quad x_2=\frac{-b+\sqrt\Delta}{2a}$$où \(\Delta=b^2-4ac\), bien entendu si \(\Delta\geq0\). Sinon, il n’y a pas de racines.
Autrement dit, \(P(x_1)=0\) et \(P(x_2)=0\) si \(x_1\) et \(x_2\) existent.
Je vous passe bien entendu l’ensemble du cours… car ce n’est pas l’objectif de cet article. Si vous souhaitez avoir une fiche complète de cours, rendez-vous sur cette page du site mathweb.fr.
À quoi sert le second degré: une application en cinétique
Quand on lance un objet vers le haut, sa trajectoire suit une courbe parabolique:
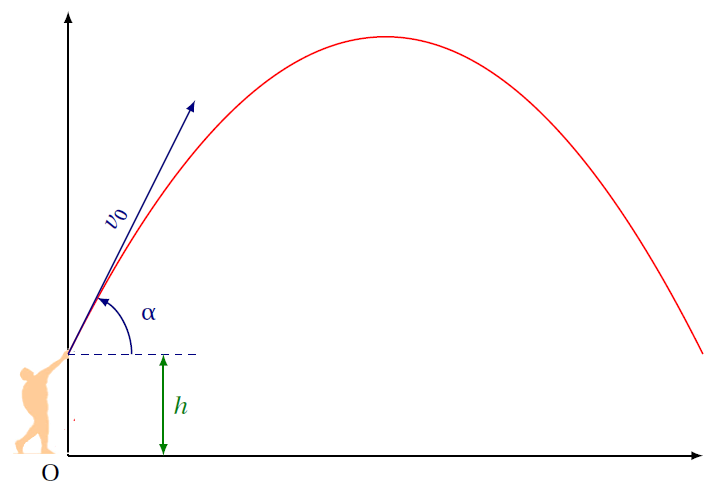
Cela signifie que l’on peut déterminer la position de l’objet lancé en fonction de la distance au sol par rapport au point initial O: donc en sachant l’abscisse.
Les lois de la mécanique newtonienne nous permettent de déterminer avec exactitude cette équation:$$-\frac{g}{2v_0^2\cos^2\alpha}x^2+(\tan\alpha)x+h$$où \(v_0\) est la vitesse à laquelle nous lançons l’objet et \(\alpha\) l’angle avec l’horizontale selon lequel on le lance (source : https://www.methodephysique.fr/equations_horaires/#parabole).
Ainsi, si l’on connaît la vitesse initiale et l’angle (ouais, c’est vrai, c’est pas facile à savoir comme ça mais on peut faire au feeling…), on peut savoir où arrivera. Mais la théorie du second degré nous permet de déterminer l’abscisse du sommet de la trajectoire (c’est plutôt sympa quand on joue au volley-ball pour être sûr·e de lancer au-dessus du filet).
À quoi sert le second degré: une application en S.V.T. (principe de Hardy-Weinberg)
On peut rencontrer le second degré dans le principe de Hardy-Weinberg.
Dans un exercice que j’ai rencontré (« Interros des lycées », SVT Terminale), on rencontre par exemple cette équation:
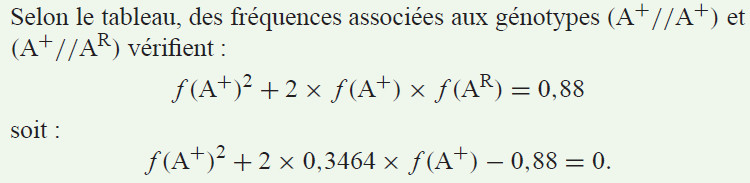
En considérant que \(f(A^+)\) est l’inconnue, on a bien une équation du second degré.
À quoi sert le second degré: une application maths sur les équations différentielles
Là, on s’éloigne du programme du lycée… Une équation différentielle (ça, c’est au programme de Terminale) est une équation où l’inconnue est une fonction que l’on a dérivé une ou plusieurs fois.
Par exemple, \(y’ + 2y = 3\) est une équation différentielle du premier ordre car l’inconnue \(y\) est une fonction qui est dérivée une fois (\(y’\)).
\(y » + 3y’ – y=0\) est en revanche une équation différentielle du second ordre. Et pour résoudre ce type d’équations, on doit résoudre son équation caractéristique, à savoir ici \(r^2+3r-1=0\). Là encore, on voit que la théorie du second degré est nécessaire.
Si la résolution en elle-même vous intéresse, jetez un coup d’œil à cette page.


Comments are closed